Cubic Bézier Curves for OpenSCAD

I like OpenSCAD. If you haven’t heard about it here is a short excerpt from it’s documentation:

OpenSCAD is a solid 3D modeler that enables creation of parametric models using its scripting language.

It is quite nice and I have already played with it. My previous project used simple constructs, mostly polygons and rotate extrude. And it was great for that. However my current project is somewhat more artsy which in this case means I wanted it to have curves. I had some experience playing with cubic Bézier curves however there was no such primitive in the language or standard library (though I haven’t looked too hard).

Bézier curves are quite easy to implement and easy/intuitive(-ish) to use.

Animation is better than thousand words, so if you don’t want to read through the whole Wikipedia article here is just the most relevant animation:

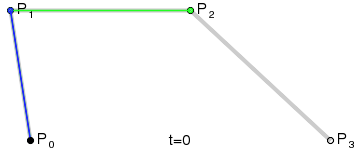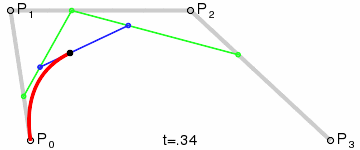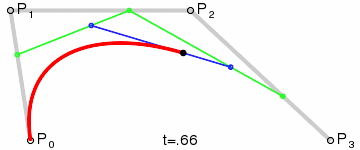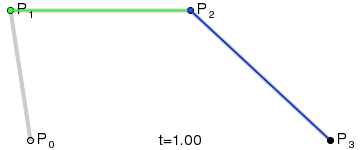
That turned out to be a nice exercise. Here is the code:

module bezier(points, extra=[], steps=$fn) {
    s = [for (pt = [0:3:len(points)-4])
        each [for (i = [0:1:steps])
           let (
                t = i/steps,
                p0 = points[pt],
                p1 = points[pt+1],
                p2 = points[pt+2],
                p3 = points[pt+3],
                p01 = (p1-p0)*t+p0,
                p12 = (p2-p1)*t+p1,
                p23 = (p3-p2)*t+p2,
                p012 = (p12-p01)*t+p01,
                p123 = (p23-p12)*t+p12,
                p0123 = (p123-p012)*t+p012)
           p0123]];

    polygon(concat(s, extra));
}

• Argument points is list of points that specify individual chunks of curve as cubic Bézier curves. The first chunk is specified by first 4 points followed by triplets of points (first point is always the last one from the previous chunk). This technically works for 2D and 3D.
• Argument extra is extra points to be added at the end without any curving, mostly useful during model creation.
• It (ab)uses special variable $fn to determine how many segments should be used to approximate each part of the whole curve.

Example use:

bezier([
    [0,0],[0,1],[2,0],[0,-1],
    [-2,0],[0,1],[0,0]
    ]);

And here is somewhat more complex example of what it can do:

Going Beyond Cubic

Cubic Bézier is usually enough for all practical purposes… However I was curious whether it would be possible to create a generic version of the function, one that would be able to approximate curve of any degree.

Also an interesting thing to notice is that modules and functions do not share a namespace so it is possible to have both a function and a module with the same name.

Function bezier_pt recursively calculates point on a curve. Function bezier breaks down provided input based on the degree.

function bezier_pt(points, t) = let (l = len(points))
    l < 2
    ? points[0]
    : bezier_pt([for (i = [0:l-2]) (points[i+1]-points[i])*t+points[i]],t);

function bezier(points, degree=3, steps=$fn) =
    [for (pt = [0:degree:len(points)-degree-1])
        each [for (i = [0:1:steps])
           bezier_pt([for (j=[pt:pt+degree]) points[j]],i/steps)
        ]
    ];

module bezier(points, degree=3, extra=[], steps=$fn) {
    polygon(concat(bezier(points, degree=degree, steps=steps), extra));
}